Heap Binomiais (parte 4)

| Parte 1 | Parte 2 | Parte 3 | Parte 4 |

Operações (continuação)

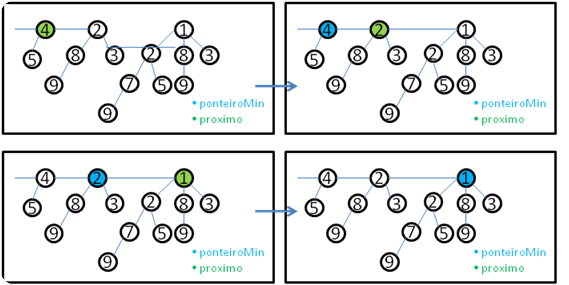
Extract_Min

Função que remove o nó com a menor chave do Heap.

ExtractMin(H){
//Nesse trecho o código busca a raiz com a menor chave e a //remove junto com as suas sub-arvores 
minimumRoot = Minimum(H)
//Caso a raiz com a chave mínima estiver no início remove-se //logo
if minimumRoot = H-head  
H-head = H-head-sibling
else{ 
//Caso contrario tem que achar a posição dela
rootSearch = H-head
while rootSearch-sibling != minimumRoot { 
rootSearch = rootSearch-sibling
}
//Depois de encontrada é removida
rootSearch-sibling = rootSearch-sibling-sibling
}
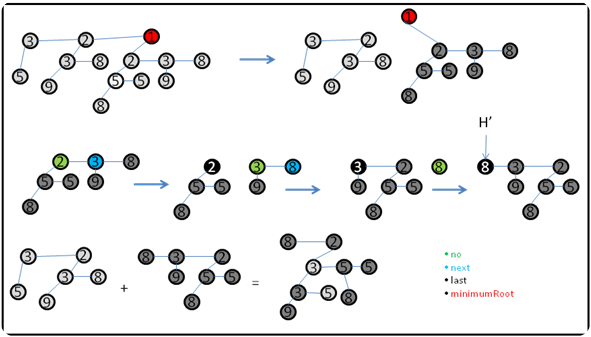
//Caso essa raiz possuir sub-árvores, devem ser devolvidas ao //Heap
if(minimumRoot-child != null){
//Inverte a ordem das sub-árvores formando um heap
H' := Make_Heap()
last = NULL
no = minimumRoot-child

//A primeira sub-arvore que deve ser a ultima
//Para ser a ultima o nó a direita deve ser null
//Varre as sub-arvores mudando os seus ponteiros, 
//os nós a direita de um determinado nó devem ser aqueles que       //estavam a sua esquerda, invertendo assim a ordem das sub-//arvores
while no != null{   
next = no-sibling
no-sibling = last
last = no
no = next
}
//O início do heap aponta para os último que estava a direita
H'-head = last
//Junta esse Heap com o original   
H = Binomial-Heap-Union(H,H') 
}
return minimumRoot
}

 

Decrease_key


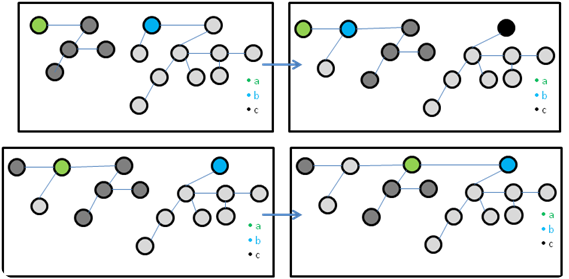
Função que diminui a chave de um nó X para um valor K e o realoca na posição correta do Heap.

Decrease_Key(H,x,k)
if k > x-key
then error "o valor é maior que a chave atual do nó"
x-key = k
atual = x
pai = atual-p
// Enquanto houver raiz e nova chave do nó for menor que a chave //do nó pai
while atual != NULL and atual-key < pai-key 
do 
troca atual-key com pai-key
//Se possui outros campos troca-se também
//Sobe a na árvore
atual = pai
pai = atual-p

Delete

Remove um nó qualquer do Heap.

Delete(H,x)
//Dado um nó qualquer torna a chave dele o menor possível e //remove-lo com a função extrair o mínimo. 
//Para atribuir o menor valor a chave pode buscar a menor chave //do Heap e decrementar um
Decrease-Key(H,x,-infinity)
Return Extract-Min(H)

Referência Bibliográfica

• Binomial Heap Wikipedia http://en.wikipedia.org/wiki/Binomial_heap
• Eduardo Camponogara Universidade Federal de Santa Catarina http://www.das.ufsc.br/~camponog/Disciplinas/DAS-9003/slides_CLR/l11-binomial-heaps.pdf
• Gabriel Pedro de Castro Unicamp http://www.ic.unicamp.br/~zanoni/mo637/aulas/heapsBinomiais.pdf
• Department Computer Science and Engineering, New York University(Animação) http://www.cse.yorku.ca/~aaw/Sotirios/BinomialHeap.html
• Binomial Trees, Bruno R. Preiss http://www.brpreiss.com/books/opus4/html/page371.html
• Algoritmos Teoria e Prática, Thomas H. Cormen Pg 365 á 379

| Parte 1 | Parte 2 | Parte 3 | Parte 4 |

Heaps Binomiais (parte 3)

| Parte 1 | Parte 2 | Parte 3 | Parte 4 |

Operações (continuação)

HeapMerge

Função que retorna uma lista de arvores binomiais de ordem de grau crescente a partir da união de dois heaps.

HeapMerge(H1,H2)
// Ambos Heaps apontam para uma raiz de menor grau, "a" apontara para o menor dessas duas raízes, "b" apontara para a outra
a = H1-head
b = H2-head
head[H1] = Min-Degree(a, b)
if H1-head = NIL
return
if H1-head = b
then b = a
a = H1-head
//Enquanto houver árvores do lado "b" continue unindo
while b != NULL do 
//Se não houver mais árvores a direita de "a", a árvore da direita de "a" será "b"
if a-sibling = NULL 
then a-sibling = b
return
else if a-sibling-degree < b-degree
//Se grau da raiz a direita de "a" for menor que grau de b, avance para "a" para o seu irmão à direita
then a = a-sibling
//Se não, precisa inserir a raiz "b" antes da raiz "a"
else c = b-sibling
b-sibling = a-sibling
a-sibling = b
a = a-sibling
b = c
return H1

Union

Função que retorna um heap a partir da união de depois heaps.

Binomial-Heap-Union(H1,H2)
H = Make_Heap()
//Monta uma lista de árvores binomiais dos dois heaps ordenadas por grau
H-head = HeapMerge(H1,H2)
//libera a memória ocupada por H1 and H2 mas não as listas que //eles apontam
if H-head = NULL
then return H
// Aqui há uma estrutura de dados X, possui os mesmos atributos //de um nó
// porém com mais dois: Prev (nó raiz da esquerda) Next (nó raiz //direita)
// Essa estrutura servirá para navegar entre as raízes e fazer //as operações
x-prev = NULL
x = H-head
x-next = x-sibling
while x-next != NULL //Enquanto houver raiz à direita
//Verifica se os graus da raiz atual e a próxima são //diferentes ou se há três raízes iguais em seqüência. Nesse //caso avança a navegação.
do if (x-degree !- next-x-degree) or
(next-x-sibling != NULL
and next-x-sibling-degree = x-degree)
then prev-x = x
x = next-x
//Se a chave da raiz atual for menor que o próximo, //a raiz atual será a nova raiz da nova árvore binomial com a //próxima raiz sendo seu filho mais a esquerda
// Não pode esquecer que a raiz a direita do próximo será a da //raiz atual
else if x-key <= next-x-key
then x-sibling = x-next-sibling 
Link(x-next,x)
//Se a chave atual for maior, o próximo nó será a nova raiz //com o nó atual sendo seu filho mais a esquerda. Dessa forma, o //nó a direita do nó anterior será o próximo nó, não havendo nó //anterior então o início da lista é o próximo nó.
else if prev-x = NIL   
then H-head = next-x
else x-prev-sibling = next-x
Binomial-Link(x,x-next)
x = x-next
x-next = x-sibling // No final sempre avança a                                     //navegação do próximo nó
return H

Insert_Heap

Função que insere um nó qualquer em um heap.

Insert_Heap(H,x)
//A idéia é muito simples, simplesmente cria-se um heap com um // único nó e usa a função de união nele 
H' = Make-Binomial-Heap()
x-p = NULL
x-child = NULL
x-sibling = NULL
x-degree = 0
H'-head = x
H = Binomial-Heap-Union(H,H')

| Parte 1 | Parte 2 | Parte 3 | Parte 4 |

Heaps Binomiais (parte 2)

| Parte 1 | Parte 2 | Parte 3 | Parte 4 |

Operações

As principais operações dos heaps binomiais e seus respectivos tempos no pior caso são:

• Make_Heap (Montar o Heap) Θ(1);
• Insert_Heap (Inserir) Θ (log2 n);
• Minimum (Mínimo) Θ(log2 n);
• Extract_Min (Extrair o mínimo) Θ(log2 n);
• Union (União) Θ(log2 n);
• Decrease_Key (Decrementar chave) Θ(log2 n);
• Delete (Excluir) Θ(log2 n).

Make_Heap

Função que cria o Heap

Make_Heap(){
H ← new no()
H-head ← NULL // Marca o pai como nulo, já que é o nível mais alto
return H
}

Minimum

Função que busca a menor chave do Heap. Tarefa fácil, já que os menores valores estão nas raízes.

Minimum(H){ // H é o Heap
ponteiroMin ← NULL
proximo ← H-head // Inicio das raízes
min ← ∞
// Varre todas as raízes e determina a menor chave
while proximo != NULL { 
if proximo-key < min {
min ← x-key
ponteiroMin ← x
}
proximo ← x-sibling
}
return ponteiroMin
}

Link

Função que une duas árvores B(k-1)

Link(y, z){
y-p ← z // Pai de y será z
// A raiz imediatamente a direita será o filho mais a esquerda de z
y-sibling ← z -child 
z-child ← y //Agora o filho mais a esquerda de z é y
// Aumenta o grau de z graças ao seu novo filho
z-degree ← z-degree + 1 
}

| Parte 1 | Parte 2 | Parte 3 | Parte 4 |

Heaps Binomiais

| Parte 1 | Parte 2 | Parte 3 | Parte 4 |

Esse post é sobre um trabalho acadêmico que fiz e ficou muito bom, bastante completo comparado as referências de outros sites. Por isso deixarei esse material de apoio para aqueles que um dia iram pesquisar sobre esse assunto.

Introdução

Para definir heaps binomiais é importante definir antes o que é uma Árvore Binomial. Árvores binomiais são formadas pela seguinte recursão:
· B(0), um vértice
· B(k) , são duas arvores binomiais B(k-1), onde a raiz de uma é o filho mais a equerda da outra.

Uma arvore binomial possui:

• 2^k nós;
• Altura k;
• nível i, possui nós, sendo i =0,1...k;
• A raiz Bk sempre terá grau k maior que todos os outros nós.

Um heap binomial é um conjunto dessas árvores binomiais com mais 2 propriedades:

• Toda árvore binomial tem a estrutura de um heap. Nos heaps, a chave de um nó é maior ou igual a chave do seu pai, assim cada nó da arvoré binomal irá possuir essa mesma propriedade.
• Outra propriedade é que dentro de um heap só pode haver uma única raiz com um determinado grau. Assim para um heap de n nós, haverá [log2 n] + 1. Uma forma mais simples é imaginar a representação binária do número de nós, por exemplo 10 é respresentado por 1010, 2^3 +2^1, assim o heap de 10 elementos será representado por duas árvores binominais B(3) e B(1).

Representação

A estrutura de dados de um nó do heap é:

•  key, onde será armazenada a chave do nó
•  p, ponteiro para o pai do nó
•  child, ponteiro para o filho mais a esquerda
• sibling, ponteiro para o irmão imediatamente à direita
•  degree, grau do nó (número de sub-árvores)
• Haverá uma estrutura do Heap que possui um ponteiro (head) para o nó inicial

| Parte 1 | Parte 2 | Parte 3 | Parte 4 |