Heaps Binomiais (parte 3)

| Parte 1 | Parte 2 | Parte 3 | Parte 4 |

Operações (continuação)

HeapMerge

Função que retorna uma lista de arvores binomiais de ordem de grau crescente a partir da união de dois heaps.

HeapMerge(H1,H2)
// Ambos Heaps apontam para uma raiz de menor grau, "a" apontara para o menor dessas duas raízes, "b" apontara para a outra
a = H1-head
b = H2-head
head[H1] = Min-Degree(a, b)
if H1-head = NIL
return
if H1-head = b
then b = a
a = H1-head
//Enquanto houver árvores do lado "b" continue unindo
while b != NULL do 
//Se não houver mais árvores a direita de "a", a árvore da direita de "a" será "b"
if a-sibling = NULL 
then a-sibling = b
return
else if a-sibling-degree < b-degree
//Se grau da raiz a direita de "a" for menor que grau de b, avance para "a" para o seu irmão à direita
then a = a-sibling
//Se não, precisa inserir a raiz "b" antes da raiz "a"
else c = b-sibling
b-sibling = a-sibling
a-sibling = b
a = a-sibling
b = c
return H1

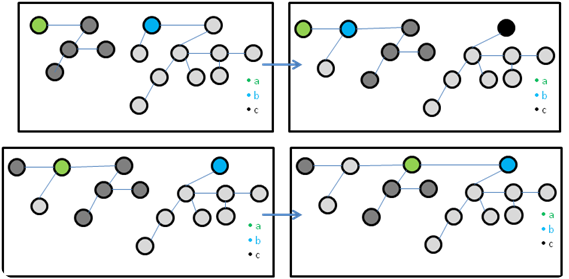
Union

Função que retorna um heap a partir da união de depois heaps.

Binomial-Heap-Union(H1,H2)
H = Make_Heap()
//Monta uma lista de árvores binomiais dos dois heaps ordenadas por grau
H-head = HeapMerge(H1,H2)
//libera a memória ocupada por H1 and H2 mas não as listas que //eles apontam
if H-head = NULL
then return H
// Aqui há uma estrutura de dados X, possui os mesmos atributos //de um nó
// porém com mais dois: Prev (nó raiz da esquerda) Next (nó raiz //direita)
// Essa estrutura servirá para navegar entre as raízes e fazer //as operações
x-prev = NULL
x = H-head
x-next = x-sibling
while x-next != NULL //Enquanto houver raiz à direita
//Verifica se os graus da raiz atual e a próxima são //diferentes ou se há três raízes iguais em seqüência. Nesse //caso avança a navegação.
do if (x-degree !- next-x-degree) or
(next-x-sibling != NULL
and next-x-sibling-degree = x-degree)
then prev-x = x
x = next-x
//Se a chave da raiz atual for menor que o próximo, //a raiz atual será a nova raiz da nova árvore binomial com a //próxima raiz sendo seu filho mais a esquerda
// Não pode esquecer que a raiz a direita do próximo será a da //raiz atual
else if x-key <= next-x-key
then x-sibling = x-next-sibling 
Link(x-next,x)
//Se a chave atual for maior, o próximo nó será a nova raiz //com o nó atual sendo seu filho mais a esquerda. Dessa forma, o //nó a direita do nó anterior será o próximo nó, não havendo nó //anterior então o início da lista é o próximo nó.
else if prev-x = NIL   
then H-head = next-x
else x-prev-sibling = next-x
Binomial-Link(x,x-next)
x = x-next
x-next = x-sibling // No final sempre avança a                                     //navegação do próximo nó
return H

Insert_Heap

Função que insere um nó qualquer em um heap.

Insert_Heap(H,x)
//A idéia é muito simples, simplesmente cria-se um heap com um // único nó e usa a função de união nele 
H' = Make-Binomial-Heap()
x-p = NULL
x-child = NULL
x-sibling = NULL
x-degree = 0
H'-head = x
H = Binomial-Heap-Union(H,H')

| Parte 1 | Parte 2 | Parte 3 | Parte 4 |