Heaps Binomiais (parte 2)

| Parte 1 | Parte 2 | Parte 3 | Parte 4 |

Operações

As principais operações dos heaps binomiais e seus respectivos tempos no pior caso são:

• Make_Heap (Montar o Heap) Θ(1);
• Insert_Heap (Inserir) Θ (log2 n);
• Minimum (Mínimo) Θ(log2 n);
• Extract_Min (Extrair o mínimo) Θ(log2 n);
• Union (União) Θ(log2 n);
• Decrease_Key (Decrementar chave) Θ(log2 n);
• Delete (Excluir) Θ(log2 n).

Make_Heap

Função que cria o Heap

Make_Heap(){
H ← new no()
H-head ← NULL // Marca o pai como nulo, já que é o nível mais alto
return H
}

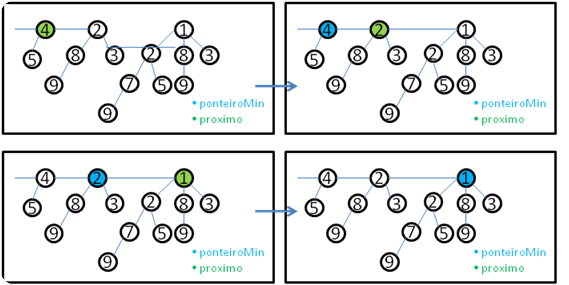
Minimum

Função que busca a menor chave do Heap. Tarefa fácil, já que os menores valores estão nas raízes.

Minimum(H){ // H é o Heap
ponteiroMin ← NULL
proximo ← H-head // Inicio das raízes
min ← ∞
// Varre todas as raízes e determina a menor chave
while proximo != NULL { 
if proximo-key < min {
min ← x-key
ponteiroMin ← x
}
proximo ← x-sibling
}
return ponteiroMin
}

Link

Função que une duas árvores B(k-1)

Link(y, z){
y-p ← z // Pai de y será z
// A raiz imediatamente a direita será o filho mais a esquerda de z
y-sibling ← z -child 
z-child ← y //Agora o filho mais a esquerda de z é y
// Aumenta o grau de z graças ao seu novo filho
z-degree ← z-degree + 1 
}

| Parte 1 | Parte 2 | Parte 3 | Parte 4 |